TFLM: Added design doc for optimized DepthwiseConv2D (vexriscv)
diff --git a/tensorflow/lite/micro/kernels/vexriscv/doc/DepthwiseConv2D_int8.md b/tensorflow/lite/micro/kernels/vexriscv/doc/DepthwiseConv2D_int8.md
new file mode 100644
index 0000000..897fc63
--- /dev/null
+++ b/tensorflow/lite/micro/kernels/vexriscv/doc/DepthwiseConv2D_int8.md
@@ -0,0 +1,136 @@
+# Design of DepthwiseConv2D for VexRISCV
+* Author: Daniel You (Google SWE intern, Summer 2020)
+* Github Profile: [danielyou0230](https://github.com/danielyou0230)
+* Last Update: August 28, 2020
+* [PR#42715](https://github.com/tensorflow/tensorflow/pull/42715) (see experiment results in the PR message)
+
+## Overview
+The kernel is optimized based on the reference kernel in Tensorflow Lite. Different from the straightforward implementation, this implementation takes memory layout in TF Lite (`NHWC`) into account, which leverages memory hierarchy to reduce memory miss count, to be more specific, it performs depthwise convolution for every channel in a fixed spatial position (iterate `C`-axis first, then `W`-axis, `H`-axis, and `N`-axis).
+
+
+## Objective
+With the debut of Artificial Intelligence (AI) products and services, our lives have been changed ever since. While much of those applications are cloud-based implementations, there are still many cases where AI algorithms have to be run on resource constrained devices. Current machine learning frameworks are still not well optimized for those platforms, thereby preventing more complicated applications running on them with acceptable performance.
+
+This design focuses on improving the performance of kernels in TensorFlow Lite Micro, to be more specific, this design involves one of the most popular kernels among the models deployed on edge devices: DepthwiseConv2D (see [TensorFlow Python API](https://www.tensorflow.org/api_docs/python/tf/keras/layers/DepthwiseConv2D); [discussion on MobileNetV1](https://groups.google.com/g/keras-users/c/sec8pYjJwwE) on Google groups.) The goal is to reduce the inference time on those devices which can in turn save more energy on them or more importantly, enable more complex applications running on them.
+
+## Background
+Existing works aim to optimize on-CPU performance focus on leveraging CPU specific instruction like SIMD instructions in RISC-V Vector and other counterparts like AVX and SSE intrinsics. An implementation released by Facebook ([pytorch/FBGEMM](https://github.com/pytorch/FBGEMM/tree/master/src)) demonstrated the potential that can be achieved with the aforementioned vector instructions.
+
+The alternative approach is to optimize on GPUs. Modern GPUs are well-known for having great performance in matrix multiplication and parallel computation (e.g. CUDA from Nvidia). Those powerful GPUs enable machine learning researchers to explore a wide variety of models and solve complicated problems. For resource constrained embedded processors, however, incorporating a GPU may not fit the limited hardware and power budget for their applications. Unlike running TensorFlow Python APIs on desktop or servers, TensorFlow Lite and TensorFlow Lite Micro are made to efficiently run inference on those devices, which enables the possibilities to make machine learning applications ubiquitous in our life.
+
+## Requirements and scale
+After detailed analysis on memory access patterns in existing implementations, I found existing code under-utilizes the memory hierarchy, specifically, the SRAM cache, to reduce excessive memory access time, which would be approximately 100 times slower if memory access were optimized ([Latency Numbers Every Programmer Should Know](https://gist.github.com/jboner/2841832), [The Effect Of CPU Caches And Memory Access Patterns](http://kejser.org/the-effect-of-cpu-caches-and-memory-access-patterns/).) Therefore, this design aims to improve the memory access pattern to better fit the memory layout of the TensorFlow Lite C++ library. Any integer-based models with DepthwiseConv2D layers using TensorFlow Lite Micro will benefit from this change.
+
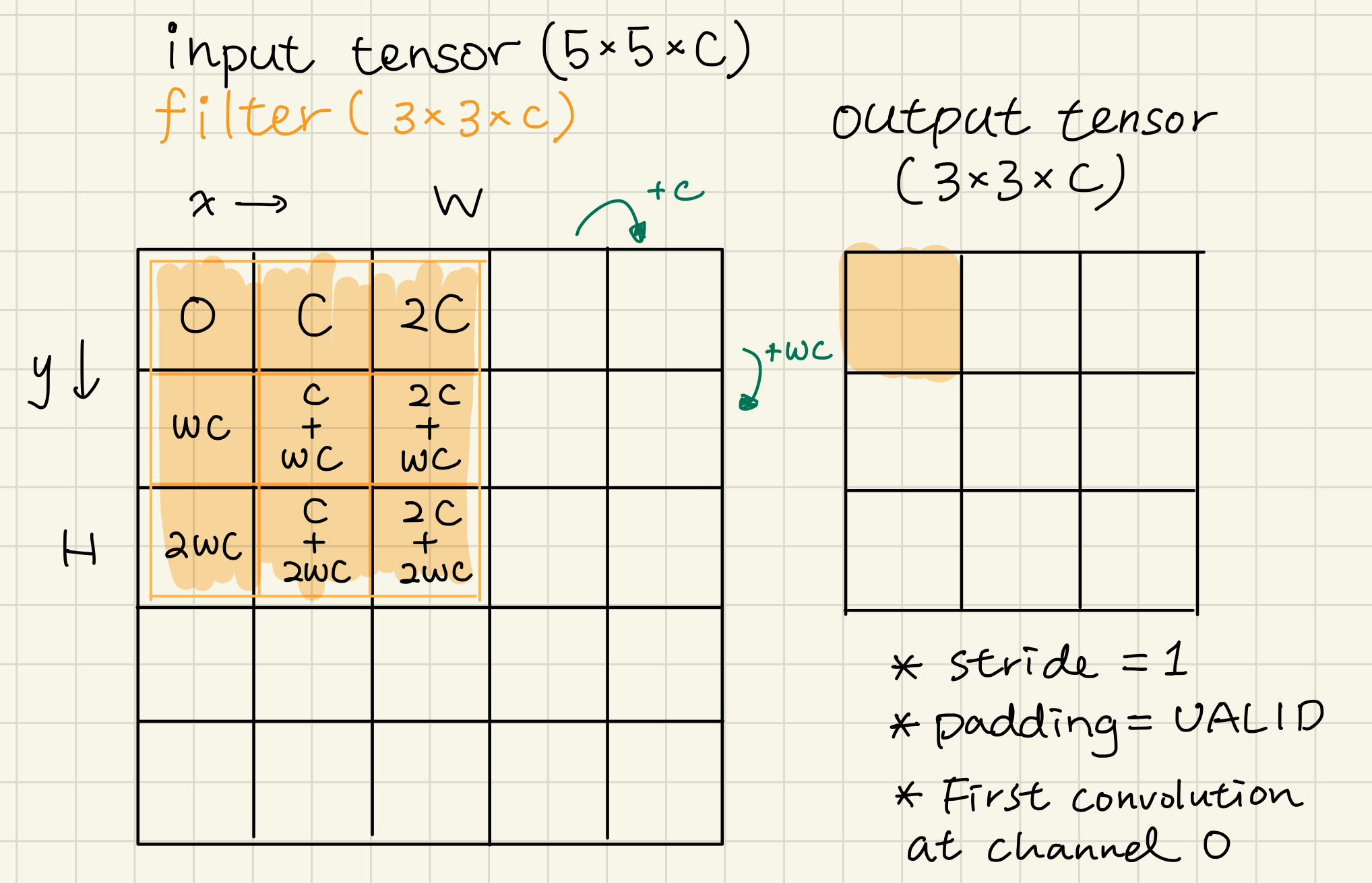
+To begin with, the memory layout of tensors in TensorFlow Lite C++ library uses `NHWC` format `(n, height, width, channel)` and flattened to an 1-d tensor, the index of `(n, h, w, c)` in the tensor can then be calculated with `((n * H + h) * W + w) * C + c`. The reference implementation is depicted as follows:
+
+```
+for i-th input among N inputs
+ for c-th input channel
+ for (y, x) in input that are convolving with the filter
+ access element (i, y, x, c) in the input
+```
+
+Thus, if the current element is `(i, y, x, c)` at index `((i * H + y) * W + x) * C + c`, next element will be `(i, y, x + 1, c)` at index `((i * H + y) * W + (x + 1)) * C + c`, the difference of indices between two consecutive accesses is `C` (illustrated below,) which is apparently not a sequential access.
+
+
+
+In response to the poor memory access pattern in the reference, it would be beneficial to implement DepthwiseConv2D in a depth-centric manner, namely, accessing elements at a fixed spatial location `(y, x)` for each channel. The access order then becomes sequential on the 1-d tensor because the layout of tensors are in the format of `NHWC`.
+
+## Design ideas
+Instead of accessing the memory in a non-sequential manner, this design proposes to change the access pattern to be consistent with the memory layout in the current TensorFlow Lite C++ library. The idea can be broken down into two major parts:
+
+* Relating sequential memory access to DepthwiseConv2D
+* Depthwise convolution with sequential memory access scheme
+
+### Relating sequential memory access to DepthwiseConv2D
+Contrary to the reference implementation, the proposed solution re-orders the calculation to access the elements sequentially in the tensor, namely, `(0, 1, 2, ..., H * W * C - 1)`. This can be done by interchanging the order of two inner loops:
+```
+for i-th input
+ for (y, x) in input that are convolving with the filter
+ for c-th input channel
+ access element (i, y, x, c) in the input
+```
+
+In this case, if the current element is `(i, y, x, c)` at index `((i * H + y) * W + x) * C + c`, the next element will be `((i * H + y) * W + x) * C + (c + 1)`, the difference of between two consecutive access becomes `1`, thereby fully re-using the data in a cache block.
+
+### Depthwise convolution with sequential memory access scheme
+In the existing TF Lite reference implementation, each element in the output is calculated by performing `(filter_h * filter_w)` multiplications and additions in a row. With the proposed design, memory access patterns can be greatly improved by re-ordering the calculations.
+
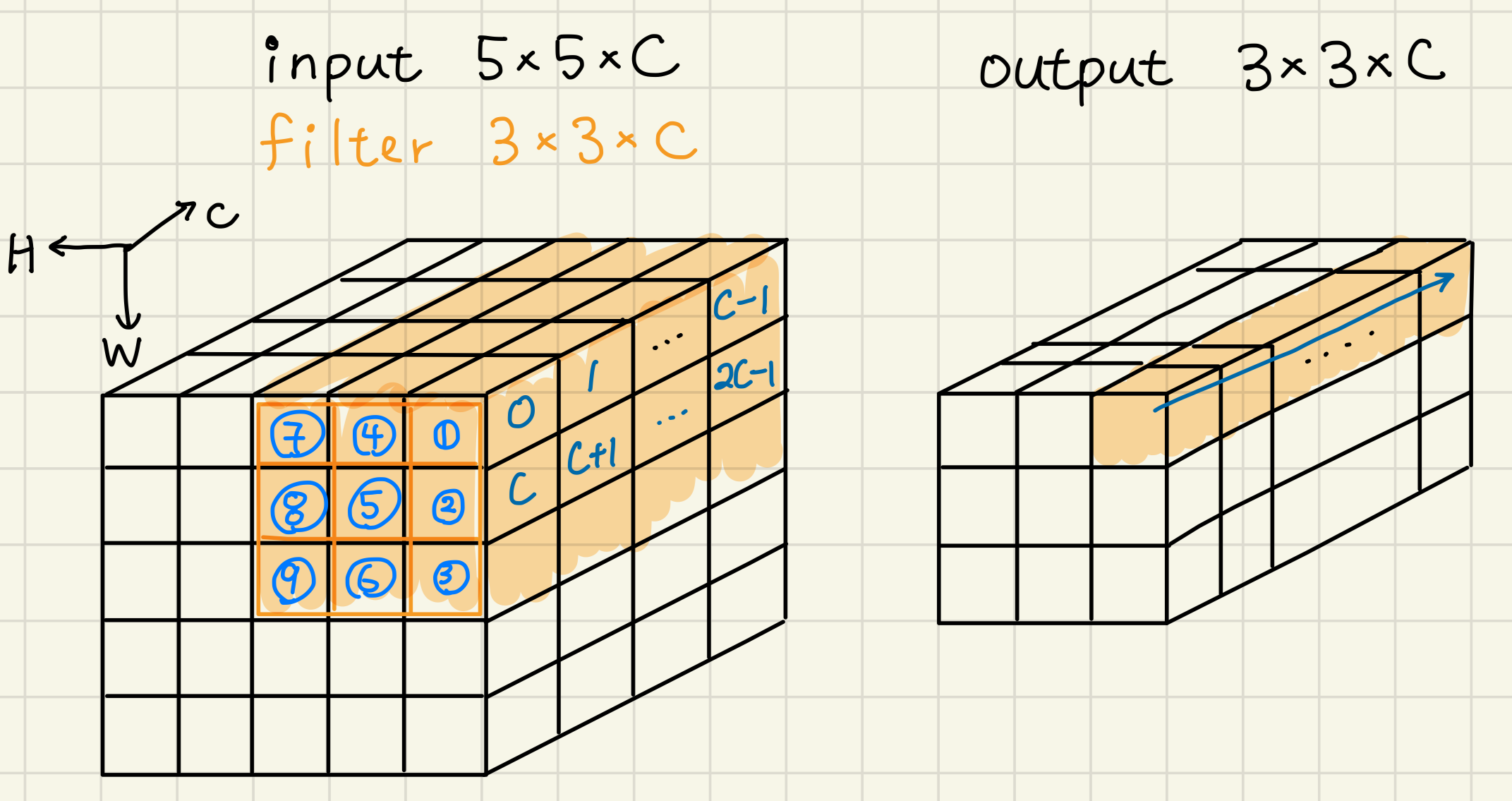
+Rather than calculating the results in a row, this design rearranges the operations. To calculate the output at a specific spatial location for all channels (see the colored cells in the output tensor in the figure below) the resulting order of calculations is illustrated below, the involving input/filter locations are represented as `(spatial index, channel)`
+
+
+
+| Original | Optimized |
+|:---------------:|:---------------:|
+| (#1, 0) | (#1, 0) |
+| (#2, 0) | (#1, 1) |
+| ... | ... |
+| **(#9, 0)** | (#1, C - 1) |
+| (#1, 1) | (#2, 0) |
+| ... | ... |
+| **(#9, 1)** | **(#9, 0)** |
+| ... | ... |
+| **(#9, C - 1)** | **(#9, C - 1)** |
+
+The calculation for each element at the output is completed when it reaches the bold coordinates in the table. From the table, this scheme only gets partial results until it reaches the last location (i.e., `(#9, 0)` to `(#9, C-1)`). Ideally, we can use the output tensor directly as an accumulator, no extra space is needed at runtime. Yet, since the output tensor is limited (8 bits) in an integer model, accumulating intermediate values at the output tensor will cause overflow: the product of two `int8` values is in the range of `int16` and there are `H * W` values to be accumulated, the range of the value before quantization is `H * W * MAX_INT16`. Therefore, an `int32` accumulator is adequate as long as the number of accumulations `(H*W*C)` does not exceed `2^16`. To address overflow when accumulating at output tensor and provide better memory access pattern, an `int32` array of size equals to number of channels (`C`) as accumulators is enough, since those `C` calculations are done once a set of spatial locations (`#1` to `#9`) are convolved, we don't have to allocate an array with size equals to the output tensor to accumulate the values.
+
+If we implement this idea, i.e. allocating a temporary array with size equals to `C`, we can follow the loop structure shown below, this would work just fine, but as we can see in the routine, it involves allocating an `int32` array of **size in proportional to the input channel**, which is not preferable in those resource limited devices because we cannot assure there will always be enough memory given any application or model.
+
+```
+for i-th input among N inputs
+ for each (out_y, out_x)
+ for m < depth_multiplier; step_size = 1
+ calculate origin (in_y_origin, in_x_origin) to perform convolution
+
+ // Accumulate partial results in buffer given a origin
+ create an int32 buffer of size output_channel as accumulators
+
+ for each (filter_y, filter_x)
+ calculate (in_y, in_x) to perform convolution
+ for in_ch < in_channel; step_size = 1
+ calculate out_ch
+ // accumulate partial results
+ buffer[ch_offset] += input[indexOf(i, y, x, in_ch)] *
+ filter[indexOf(0, f_y, f_x, out_ch)]
+
+ for in_ch < in_channel; step_size = 1
+ calculate out_ch
+ // Add bias / activation / requantize
+ value = postAccumulation(buffer[out_ch])
+ output[indexOf(i, out_y, out_x, out_ch)] = value
+
+```
+
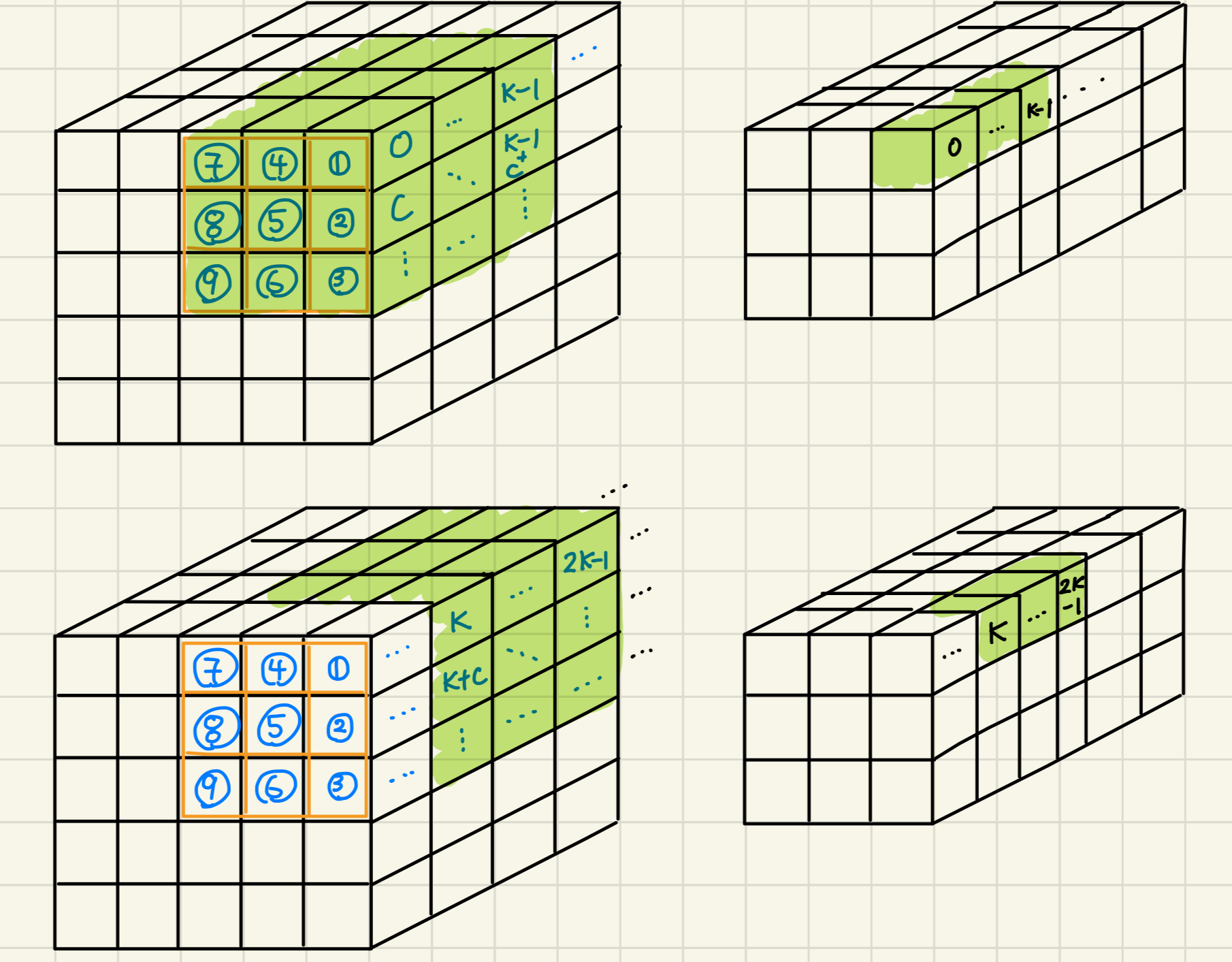
+Instead, we can further breakdown the structure into chunks, namely, we can add an additional nested loop inside to iterate `K` channels a time until all channels are processed, the modified loop structure is depicted below and the visualization is shown in the figure below the loop.
+
+```
+for i-th input among N inputs
+ for each (out_y, out_x)
+ for m < depth_multiplier; step_size = 1
+ calculate origin (in_y_origin, in_x_origin) to perform convolution
+
+ // Accumulate partial results in buffer for K channels given a origin
+ for ch < input_ch; step_size = K
+ create an int32 buffer of size K as accumulator for current chunk
+
+ for each (filter_y, filter_x)
+ calculate (in_y, in_x) to perform convolution
+ for ch_offset < channel_step; step_size = 1
+ calculate in_ch and out_ch
+ // accumulate partial results
+ buffer[ch_offset] += input[indexOf(i, y, x, in_ch)] *
+ filter[indexOf(0, f_y, f_x, out_ch)]
+
+ for ch_offset < channel_step; step_size = 1
+ // Add bias / activation / requantize
+ value = postAccumulation(buffer[ch_offset])
+ output[indexOf(i, out_y, out_x, out_ch)] = value
+
+```
+
+
+
+The final problem is how the choice of `K`, according to the soft-CPU configuration, we have a cache size of 4KB and each memory block is 32 bytes. Combined with the input format we use (`int8`) whenever the OS fetches a block of input tensor, it loads 32 `int8` to the cache. To fully utilize that block, we can choose the size of the buffer to accommodate 32 partial results (128 byte, or 4 blocks,) most applications keep the number of channels to be power of 2s (except for the input,) 32 is a reasonable value to perform depthwise convolution for both small and large numbers of channels in the model.
+
+## Alternatives considered
+An alternative design is to dynamically allocate a buffer for each channel (an `int32` array of size equals to number of output channels.) This approach is easier to implement since after `H * W * C` calculations, we can requantize those `C` values and store them into the output tensor. However, we are running on memory constrained devices, dynamic allocation is not encouraged by the upstream developers.